嗯刷

Day 1 寻找两个有序数组的中位数

给定两个大小为 m 和 n 的有序数组 nums1 和 nums2。
请你找出两个有序数组的中位数，并且要求算法的时间复杂度为O(log(m+n))
你可以假设 nums1 和 nums2 不会同时为空。

示例1：

1
2
3
4
nums1 = [1, 2]
nums2 = [2]

// 则中位数是 2.0

示例2:

1
2
3
4
nums1 = [1, 2]
nums2 = [3, 4]

// 则中位数是 (2 + 3) / 2 = 2.5

由于时间复杂度有log，因此很容易想到使用二分法。
由于是求中位数，因此我们可以换个思路，即求排列第 k 位的数。

假设我们我们要找第k位数，我们可以每次循环剔除k/2个数。

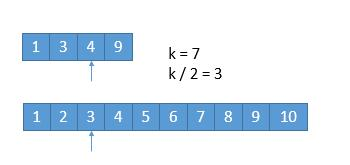
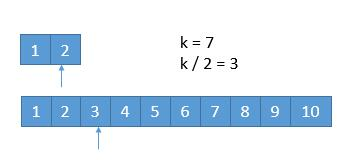
假设我们要找第7位小的数字

我们比较数组的第 k/2 个数字，如果k是奇数，则向下取整。也就是比较两个数组的第3个数字。如果哪个数组的前 k/2个数字都不会是中位数，因此可以排除掉。如上图中的1，2，3都可以排除掉。

橙色的部分表示已经去掉的数字

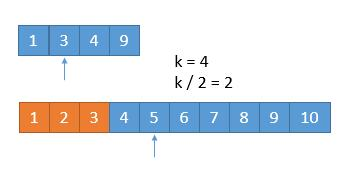
这时，我们只需要寻找新数组中的第 7 - 3 个数字，也就是k = 4。由于3 < 5，所以上面数组的前两个数字1 3 out。

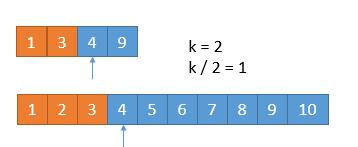
现在k = 2，我们只需找到第2小的数字即可。比较两个数组中的 k / 2 = 1个数，由于4 = 4，因此无论去掉哪个数组的都行，假设我们去掉下面那个数组的4。

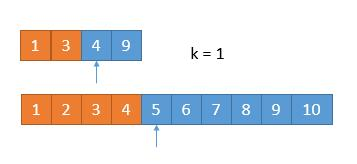
此时，k = 1，只需要判断一下两个数组哪个数字小就可以了，也就是4。

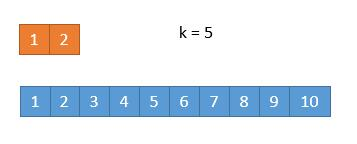
我们每次都选 k / 2，但有时会遇到数组小于 k / 2的情况。

这时，我们只需指向该数组的末尾，即2。

2、3被去除，因此下一个k = 7 - 2，即5，只需返回下面数组的第5个数字。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
/**
 * @param {number[]} nums1
 * @param {number[]} nums2
 * @return {number}
 */

var getKth = function(nums1, start1, end1, nums2, start2, end2, k) {
  const len1 = end1 - start1 + 1;
  const len2 = end2 - start2 + 1;
  if (len1 > len2) {
    return getKth(nums2, start2, end2, nums1, start1, end1, k);
  }
  
  // 当第一个数组为空，则可以直接从第二个数组中取出第k个数
  if (len1 === 0) {
    return nums2[start2 + k - 1];
  }
  
  // 当 k = 1 时，比较两个数组位于k位置的大小的最小值
  if (k === 1) return Math.min(nums1[start1], nums2[start2]);
  
  const i = start1 + Math.min(len1, parseInt(k / 2)) - 1;
  const j = start2 + Math.min(len2, parseInt(k / 2)) - 1;
  
  if (nums1[i] > nums2[j]) {
    // 此时已剔除掉 j - start2 + 1 个元素，因此k大小需要减去j - start2 + 1
    return getKth(nums1, start1, end1, nums2, j + 1, end2, k - (j - start2 + 1));
  } else {
    return getKth(nums1, i + 1, end1, nums2, start2, end2, k - (i - start1 + 1));
  }
  
}

var findMedianSortedArrays = function(nums1, nums2) {
  const n = nums1.length;
  const m = nums2.length;
  
  return (getKth(nums1, 0, n - 1, nums2, 0, m - 1, parseInt((n + m + 1) / 2) ) + getKth(nums1, 0, n - 1, nums2, 0, m - 1, parseInt((n + m + 2) / 2))) / 2;
};

Day2 最长回文字串

给定一个字符串 s，找到 s 中最长的回文子串。你可以假设 s 的最大长度为 1000

示例1:

1
2
3
输入: "babad"
输出: "bab"
注意: "aba" 也是一个有效答案。

示例2:

1
2
输入: "cbbd"
输出: "bb"

中心扩展算法

该算法可以从每个中心点向两边进行扩展，计算每个中心点可以扩展的最长回文串。值得注意的是，每个字符串都有2n - 1个中心点。因为中心点不止在字符上，两个字符的空隙也算一个中心点（比如”abba”），因此有n + (n - 1)个中心点。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
/**
 * @param {string} s
 * @return {string}
 */
var longestPalindrome = function(s) {
    if(s == null || s.length < 1) return '';
    let start = 0;
    let end = 0;
    for (let i = 0; i < s.length; i++) {
        let len1 = expandFromCenter(s, i, i);
        let len2 = expandFromCenter(s, i, i+1);
        let len = Math.max(len1, len2);
        if (len > end - start) {
            start = i - parseInt((len - 1)  / 2);
            end = i + parseInt(len / 2);
        } 
    }
    
    return s.substring(start, end + 1);
};

const expandFromCenter = function(s, left, right) {
    while (left >= 0 && right < s.length && s.charAt(left) === s.charAt(right)) {
        left --;
        right ++;
    }
    return right - left - 1;
}

动态规划

动态规划比扩展中心算法稍微难理解一点。

首先定义P(i, j):

并且 P(i,j) = (P(i + 1, j - 1) && s[i] === s[j])

如果我们想知道s[i][j]是否是回文串，那么我们只需知道s[i+1][j-1]是否回文串并且s[i] === s[j]。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
/**
 * @param {string} s
 * @return {string}
 */
var longestPalindrome = function(s) {
    const len = s.length;
    let maxLen = 0;
    let maxStr = '';
    let db = new Array(len).fill(0);
    for (let i = 0; i < len; i++) {
        db[i] = new Array(len).fill(false);
    }
    // 根据长度遍历
    for (let l = 1; l <= len; l++) {
        for (let start = 0; start < len; start++) {
            
            let end = start + l - 1;
            // end下标越界
            if (end >= len) {
                break;
            }
            
            // 单独判断长度为1和2的子串
            db[start][end] = (l === 1 || l === 2  || db[start + 1][end - 1]) && s[start] === s[end];
            
            if (db[start][end] && maxLen < l) {
                maxLen = l;
                maxStr = s.substring(start, end + 1);
            }
        }
    }
    
    return maxStr;
};

Manacher算法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
/**
 * Manacher算法
 * @param {string} s
 * @return {string}
 */
var longestPalindrome = function(s) {
  const T = s;
  s = preProcess(T);
  const length = s.length;
  let p = new Array(length).fill(0);
  // C - 到目前为止扩展到最右边的中心点
  // R - 到目前为止扩展到的最右边
  let C = 0;
  let R = 0;
  for(let i = 0; i < length; i++) {
    // 计算i根据C的对称点 i - C = C - i_mirror -> i_mirror = 2 * C - i;
    const i_mirror = 2 * C - i;
    // 如果R > i, 则可以使用p[i] = Math.min(p[i_mirror], R - i) 公式
    // 取最小值是怕i + p[i_mirror] 超过了 R， 而超过R的这部分不能保证和i_mirror一样对称。
    if (R > i) {
      p[i] = Math.min(p[i_mirror], R - i);
    } else {
      p[i] = 0;
    }
    
    // 进行中心扩展
    while(s[i + p[i] + 1] === s[i - p[i] - 1]) {
      p[i]++ ;
    }
    
    // 如果有更右边的R, 则更新C、R
    if (R < i + p[i]) {
      C = i;
      R = i + p[i];
    }
  }
  
  // 求出p中最大值
  let maxIndex = 0;
  let max = 0;
  p.forEach((item, i) => {
    if (item > max) {
      max = item;
      maxIndex = i;
    }
  })
  
  const start = (maxIndex - max) / 2;
  return T.substring(start, start + max);
};

// 在字符串中插入字符，解决奇数和偶数的问题
const preProcess = function(s) {
  const len = s.length;
  if (!len) return '^$';
  
  s = s.split('').join('#');
  s = `^#${s}#$`;
  return s;
}

Day3 有效的括号

给定一个只包括 ‘(‘，’)’，’{‘，’}’，’[‘，’]’ 的字符串，判断字符串是否有效。
有效字符串需满足：
左括号必须用相同类型的右括号闭合。
左括号必须以正确的顺序闭合。
注意空字符串可被认为是有效字符串。

示例1：

1
2
输入: "()"
输出: true

示例2：

1
2
输入: "([)]"
输出: false

这道题用了两个栈（其实一个栈就可以），遍历该字符串：

  1. 如果是右边括号，如),],}，则压入右边的栈中；
  2. 如果是左边括号，则取出右边的栈顶与之匹配，如果不能匹配则认为无效；
    当字符串遍历结束后，判断右边栈是否为空，如果为空则说明能够全部匹配；否则认为不能全部匹配，则无效。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
/**
 * @param {string} s
 * @return {boolean}
 */

const Left = ['(', '[', '{'];
const Right = [')', ']', '}'];
var isValid = function(s) {
    const stack1 = s.split('');
    const stack2 = [];
    while(stack1.length > 0) {
        const curSign = stack1.pop();
        // 如果是右边括号 则压入satck2栈中等待匹配
        if (Right.includes(curSign)) {
            stack2.push(curSign);
        } else {
            // 左边括号 则与目前stack2栈顶匹配 如果无法匹配则返回false
            const matchSign = stack2.pop();
            // 判断两个括号是否有相同的下标
            if (Left.indexOf(curSign) !== Right.indexOf(matchSign)) {
                return false;
            }
        }
    }
    return !stack2.length;
};

Day 4 合并两个有序链表

将两个升序链表合并为一个新的 升序 链表并返回。新链表是通过拼接给定的两个链表的所有节点组成的。

示例：

1
2
输入：1->2->4, 1->3->4
输出：1->1->2->3->4->4

暴力法

每次比较两个链表目前头节点的大小，选择小的作为下个当前节点。

听说大部分夏令营都是用java机试，所以就用java答题吧。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode() {}
 *     ListNode(int val) { this.val = val; }
 *     ListNode(int val, ListNode next) { this.val = val; this.next = next; }
 * }
 */
class Solution {
    public ListNode mergeTwoLists(ListNode l1, ListNode l2) {
      if (l1 == null) {
        return l2;
      }
      if (l2 == null) {
        return l1;
      }
      // 先创建一个哑节点
      ListNode dummyHead = new ListNode(0);
      ListNode cur = dummyHead;

      while (l1 != null && l2 != null) {
        if(l1.val <= l2.val) {
          cur.next = l1;
          cur = l1;
          l1 = l1.next;
        } else {
          cur.next = l2;
          cur = l2;
          l2 = l2.next;
        }

        if (l1 == null) {
          cur.next = l2;
        }
        if (l2 == null) {
          cur.next = l1;
        }
      }
      return dummyHead.next;
    }
}

递归法

我们可以如下递归地定义两个链表里的merge操作：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
    public ListNode mergeTwoLists(ListNode l1, ListNode l2) {
        if (l1 == null) {
            return l2;
        }
        else if (l2 == null) {
            return l1;
        }
        else if (l1.val < l2.val) {
            l1.next = mergeTwoLists(l1.next, l2);
            return l1;
        }
        else {
            l2.next = mergeTwoLists(l1, l2.next);
            return l2;
        }

    }
}

Day5 单词接龙

给定两个单词（beginWord 和 endWord）和一个字典，找到从 beginWord 到 endWord 的最短转换序列的长度。转换需遵循如下规则：

每次转换只能改变一个字母。
转换过程中的中间单词必须是字典中的单词。
说明:

如果不存在这样的转换序列，返回 0。
所有单词具有相同的长度。
所有单词只由小写字母组成。
字典中不存在重复的单词。
你可以假设 beginWord 和 endWord 是非空的，且二者不相同。

示例：

1
2
3
4
5
6
7
8
9
输入:
beginWord = "hit",
endWord = "cog",
wordList = ["hot","dot","dog","lot","log","cog"]

输出: 5

解释: 一个最短转换序列是 "hit" -> "hot" -> "dot" -> "dog" -> "cog",
     返回它的长度 5。

这道题主要是构建一个无向无权图，然后用广度优先搜索来找到beginWord到endWord的距离。

算法中最重要的步骤是找出相邻的节点，也就是只差一个字母的两个单词。为了快速的找到这些相邻节点，我们对给定的 wordList 做一个预处理，将单词中的某个字母用 代替。
这个预处理帮我们构造了一个单词变换的通用状态。例如：Dog —-> Dg <—- Dig，Dog 和 Dig 都指向了一个通用状态 D*g。

这步预处理找出了单词表中所有单词改变某个字母后的通用状态，并帮助我们更方便也更快的找到相邻节点。否则，对于每个单词我们需要遍历整个字母表查看是否存在一个单词与它相差一个字母，这将花费很多时间。预处理操作在广度优先搜索之前高效的建立了邻接表。

例如，在广搜时我们需要访问 Dug 的所有邻接点，我们可以先生成 Dug 的所有通用状态：

  1. Dug => *ug
  2. Dug => D*g
  3. Dug => Du*

第二个变换 D*g 可以同时映射到 Dog 或者 Dig，因为他们都有相同的通用状态。拥有相同的通用状态意味着两个单词只相差一个字母，他们的节点是相连的。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
class Solution {
    public int ladderLength(String beginWord, String endWord, List<String> wordList) {
      int L = beginWord.length();
      // 这里先构建一个单词的通用状态 h*t -> hit, hot
      Map<String, List<String>> allComboDict = new HashMap<>();

      wordList.forEach(
        word -> {
          for (int i = 0; i < L; i++) {
            String newWord = word.substring(0, i) + '*' + word.substring(i+1, L);
            List<String> transformations = allComboDict.getOrDefault(newWord, new ArrayList<>());
            transformations.add(word);
            allComboDict.put(newWord, transformations);
          }
        }
      );
      
      // 构建一个队列用于广度优先搜索
      Queue<Pair<String, Integer>> Q = new LinkedList<>();
      Q.add(new Pair(beginWord, 1));

      // 构建一个是否已访问的Map
      Map<String, Boolean> visited = new HashMap<>();
      visited.put(beginWord, true);

      while(!Q.isEmpty()) {
        // 取出队列的第一个节点
        Pair<String, Integer> node = Q.remove();
        String word = node.getKey();
        int level = node.getValue();
        for (int i = 0; i < L; i++) {
          String newWord = word.substring(0, i) + "*" + word.substring(i+1, L);
          // 获得只改变一个字母的字符串队列
          for(String adjacentWord : allComboDict.getOrDefault(newWord, new ArrayList<>())) {
            // 如果该字符串和最终结果一样，则直接返回level + 1
            if (adjacentWord.equals(endWord)) {
              return level + 1;
            }
            if (!visited.containsKey(adjacentWord)) {
              visited.put(adjacentWord, true);
              Q.add(new Pair(adjacentWord, level + 1));
            }
          }
        }
      }
      return 0;
    }
}

Day6 爬楼梯

假设你正在爬楼梯。需要 n 阶你才能到达楼顶。

每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢？

注意：给定 n 是一个正整数。

示例1：

1
2
3
4
5
输入： 2
输出： 2
解释： 有两种方法可以爬到楼顶。
1.  1 阶 + 1 阶
2.  2 阶

示例2：

1
2
3
4
5
6
输入： 3
输出： 3
解释： 有三种方法可以爬到楼顶。
1.  1 阶 + 1 阶 + 1 阶
2.  1 阶 + 2 阶
3.  2 阶 + 1 阶

看到题目首先想到的是递归，但由于重复计算太多了，超时了。用动态规划可以解决超时的问题。

1
2
3
4
5
6
7
8
9
10
11
class Solution {
    public int climbStairs(int n) {
      int [] dp = new int[n+1];
      dp[0] = 1;
      dp[1] = 1;
      for (int i = 2; i <= n; i++) {
        dp[i] = dp [i-1] + dp[i-2];
      }
      return dp[n];
    }
}

Day7 转变数组后最接近目标值的数组和

给你一个整数数组 arr 和一个目标值 target ，请你返回一个整数 value ，使得将数组中所有大于 value 的值变成 value 后，数组的和最接近 target （最接近表示两者之差的绝对值最小）。

如果有多种使得和最接近 target 的方案，请你返回这些整数中的最小值。

请注意，答案不一定是 arr 中的数字。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
// 二分查找
class Solution {
    public int findBestValue(int[] arr, int target) {
      int result = 0;
      int gap = Integer.MAX_VALUE;
      int L = 0, R = 0;
      for (int item : arr) R = Math.max(R, item);
      while (L <= R) {
        int mid = (L + R) / 2;
        
        int sum = sumArr(arr, mid);
        int currentGap = Math.abs(sum-target);
        // 如果记录的差距小于当前的差距 则更新记录 并把result更新为mid
        if (gap > currentGap) {
          gap = currentGap;
          result = mid;
        }
        // 如果两个差距相等 则取最小值
        if (gap == currentGap && result > mid) {
          result = mid;
        }
        // 和小于目标 去掉右边区间
        if (sum > target) R = mid - 1;
        // 和大于目标 去掉左边区间
        if (sum < target) L = mid + 1;
        // 和相同 直接返回结果
        if (sum == target) return mid;
      }
      return result;
    }
    public int sumArr(int[] arr, int value) {
      int sum = 0;
      for (int item : arr) {
        if (item > value) {
          sum += value;
        } else {
          sum += item;
        }
      }

      return sum;
    }
}